Paralelné vedecké výpočty: Projekty

Igor Odrobina 2003

Všeobecné pokyny

Projekt pozostáva z dvoch častí a to zostrojenia programu a vypracovaním stručnej správy. Je vhodné aby program bol písaný v jazyku C (C++) s použitím knižníc jednoducho dostupných v prostredí Linux. Na úlohy s paraleným kódom je doporučený kompilátor C++ firmy Intel, ktorý podporuje príkazy OpenMP. Tento kompilátor je pre Linux šírený zdarma a dá sa získať zo stránok fy. Intel. Prípadne tento problém treba konzultovať s vyučujúcim.

Štruktúra programu

Program by mal pri jednom spustení dať tabuľku (zoznam) časov výpočtu pri rozličných parametroch úlohy (napr. rôzne rozmery matice, vektora+veľkosť bloku). Typický čas by mal byť prepočítaný na jednu operáciu, respektíve jednu typickú operáciu. Napr. čas charakterizujúci násobenie matíc NxN by mohol byť vypočítaný

čas= celkový_čas/N/N/N/RepeatN

kde RepeatN je premená diskutovaná nižšie.

Celkový výstup by mohol mať napr. tvar:

	N=1024	N=4096	N=16386
BlokN=256	xx.xns	xx.x ns	xx.x ns
BlokN=1024		xx.x ns	xx.x ns
BlokN=4096			xx.x ns

Výsledok by mal byť zobraziteľný graficky napr. tabuľkovým kalkulátorom

Ohodnotenie času

Meranie času zabezpečte najlepšie použitím knižnice resource.h

Ak testovaná operácia príliš rýchla (napr. násobenie matíc malých rozmerov) zabezpečte násobné vykonanie (RepeatN-krát), aby čas výpočtu zabral minimálne 0.1s. (Meranie času v operačnom systéme unix je nepresné, odhadovaná presnosť može byť na úrovni 1ms, môžete uviesť vlastný odhad)

Použitie OpenMP

Toto rozšírenie umožnujúce jednoduchú paralelizáciu časti kódu cez generovanie skupiny threadov. Tieto thready OS môže spustiť na viacerých procesoroch.

-kód má byť flexibilný a funkčný nezávisle od počtu zvolených threadov,

pričom predpokladané počty threadov sú 1, 2, 4, 8, 16

-môžete predpokladať, že rozmer polí je delitelný týmito číslami

-počet threadov sa nastavuje premennou shellu OMP_NUM_THREADS

Z rozšírenia OpenMP sa sústredte na využitie príkazov

parallel

atomic

critical

private

shared

z run-time funkcií v prostredí OpenMP (omp.h) na funkcie

omp_get_num_threads()

omp_get_thread_num()

Modelové príklady sa dajú získať z nadradenej webovskej stránky. Nachádzajú v položke Príklady (pod riadkom Špecifikácia OpenMP).

Dokumentácia ku kompilátoru sa nachádza v nadradenej stránke v položke Intel C++.

Vypracovanie/obsah správy

Správa (rozsahu 2-xxx) strán, by orientačne mala osahovať:

-meno, priezvisko, špecializácia, dátum

-stručný teoretický úvod (konspekt z prednášky v LS alebo z prednášky Tao Yang)

-popis granularity kódu a dát

-vyjadrenie sa k procesu tvorby programu-analýza problému+design+implementácia.

-správa môže byť písaná principiálne aj v ASCII

-očakávané správanie výkonnosti pri použití dvoch a viacerých procesorov SMP.

(očakávanie zapojenia viacerých procesorov môže byť aj negatívne, tzn. že môže dôjsť aj k spomaleniu kódu).

-diagramy a tabuľky sú vítané

Možné témy na ďalšiu diskusiu:

-správanie sa kódu pri použití prepínačov kompilátora

-použitie rôznych kompilátorov

Konkrétne projekty

Projekt č. 1: Paralelné násobenie matíc

Paralelné násobenie matíc pri riadkových blokoch a štvorcových blokoch. Naprogramujete s použitím OpenMP. Porovnajte so sekvenčným algoritmom. (Prednáška Tao Yang, kapitola 6.1, 6.2, 6.3 a 6.5)

Projekt č. 2: Gausová eliminácia bez hľadania pivotu

Doprednú eliminačnú časť Gausovej eliminácie naprogramujete paralelne použijúc OpenMP. „Load balancing“ zabezpečte použitím cyklického mapovania. (Tao Yang kapitola 7.1.2, a 4.3)

Projekt č. 3: Paralelné riešenie tridiagonálnej sústavy rovníc „odd-even“ algoritmom.

Gausova eliminácie pre tri-diagonálneho systému neobsahuje možnosť paralelizácie. Rovnice systému sa redukciou upravia a vytvoria výpočtový strom, ktorý umožňuje paralelizáciu. Porovnajte sekvenčný a paralelný čas; odhadnite podmienky, kedy „odd-even“ algoritmus je rýchlejší ako výpočet gausovou elimináciou pre 3-diagonálne systémy (Tao Yang 11.2) (tzv. faktorizáciou).

Projekt č. 4. Sekvenčný výpočet Euklidovskej normy matice a násobenia matíc-štúdium vplyvu parametrov cache a cache-line.

Podúloha A: Euklidovská norma

-euklidovská norma by mala byť počítaná v dvoch variantoch-po riadkoch a po stĺpcoch.

Podúloha B: Násobenie matíc

Matica môže byť násobená po riadkových a stĺpcových blokoch, štvorcových blokoch.

Porovnajte trvanie súčinu s prípadom obyčajného násobenia, násobenia matice s transponovanou (riadky sa násobia s riadkami plne využijúc cache line). Zistite faktor urýchlenia úlohy.

-veľkosť cache je orientačne 128kB resp. 256kB

-veľkosť cacheline je 32B, 64B, 128B

Opcia k podúlohe B: Implementujte súčet vektorov s použitím explicitnej vektorizácie s využitím procesoru Pentium 4 a kompilátora Intel C++ (príkazy SSE, SSE2).

Projekt č. 5 Riešenie parciálnej hyperbolickej rovnice

Dvojrozmerná hyperbolická rovnica prvého rádu má tvar:

pre dva rozmery:

stabilnú numerická schéma pre konštantné V_x, V_y>0 napíšeme cez tzv. rozštiepenie operátora na x-ovú a y-ovú časť. Z časovej vrstvy k vypočítame časovú vrstvu k+1 s použitím medzikroku n^k+1/2.

CFL podmienka stability limituje veľkosť časového kroku vťahom:

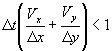
Náčrt dvojrozmernej siete

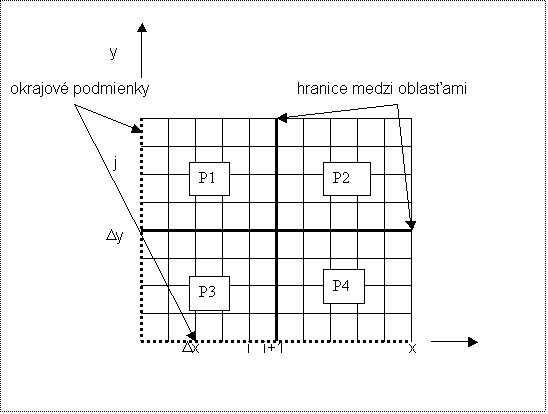
Po každom časovom kroku k nasleduje komunikácia, kedy susedné procesory(procesy) si vymieňajú hraničné dáta.

Úlohy:

1. Navrhnite rôzne delenia dvojrozmernej siete pre rôzny počet procesorov (threadov).

Vypočítajte pomer komunikácie medzi procesormi k počtu aritmetických operácií. Stanovte vzťah „surface-to-bulk-ratio“ pre rôzne prípady.

2. Vypracujte diagram výpočtu a komunikácie.

3. Napíšte jednoduchý simulačný program s využitím OpenMP.

Poznámky:

1. Uvedená numerická schéma má prvý rád presnosti a je zaťažená chybou, ktorá sa nazýva numerická difúzia.

2. Analogický problém sa používa na benchmark superpočítačov (ASCI Q). Použitý kód (SAGE) obsahuje adaptívne zjemňovanie siete a je druhého rádu presnosti. Test

je dokumentovaný na http://www.c3.lanl.gov/~fabrizio/papers/sc01.pdf